Vorbemerkungen
Wenn ein Unternehmer bei einer Bank ein Darlehen zur Finanzierung von Investitionen (z.B. Maschinen, Grundstücke oder Vorräte) aufnimmt, muss er der Bank für das überlassene Geld Zinsen zahlen. Diese gezahlten Fremdkapitalzinsen stellen in der Finanzbuchhaltung Aufwand dar. Sie verringern den handelsrechtlichen und steuerlichen Gewinn.
Wenn jedoch ein Unternehmer das benötigte Kapital aus seinem Privatvermögen in sein Unternehmen einbringt und hierfür keine Zinsen verlangt (z.B. als Eigenkapital oder als zinsloses Darlehen), entsteht dem Unternehmen tatsächlich kein Aufwand, der in der Finanzbuchhaltung erfasst werden müsste. Dennoch sind in der Kostenrechnung fiktive „kalkulatorische Zinsen“ anzusetzen.
Für den Ansatz von kalkulatorischen Zinsen sprechen folgende Erwägungen:
- Durch die zinslose Zurverfügungstellung des Kapitals kann der Unternehmer seine Mittel nicht für eine andere Anlage nutzen; es entgehen ihm also die Zinsen, die er sonst am Kapitalmarkt erzielen könnte (sog. „Opportunitätskosten“).
- Hierdurch wird vermieden, dass die Selbstkosten von der Finanzierungsstruktur eines Unternehmens abhängen.
Die kalkulatorischen Zinsen können nach folgenden Methoden berechnet werden, nämlich nach
- der Restwertmethode,
- der Durchschnittsmethode und
- dem Ansatz des betriebsnotwendigen Kapitals.
Restwertmethode
Bei der Restwertmethode wird ein kalkulatorischer Zinssatz auf den durchschnittlichen Wert der Bindung des Eigenkapitals zur Finanzierung eines Wirtschaftsgutes zum Ende innerhalb eines Wirtschaftsjahres angesetzt.
Mit dem Ansatz eines durchschnittlichen Wertes sollen Schwankungen im Wertansatz des Wirtschaftsgutes (insbesondere aufgrund von Abschreibungen) ausgeglichen werden; er bemisst sich nach folgender Formel:
durchschnittlicher Wert = (Wert zu Beginn des WJ + Restbuchwert zum Ende des WJ) / 2
Für die Bestimmung der Höhe des kalkulatorischen Zinssatzes gibt es keine festen Regeln; er orientiert sich häufig an den landesüblichen Kapitalmarktzinssätzen (oftmals zuzüglich eines Risikoaufschlagsatzes).
Hieraus ergibt sich folgende Formel:
kalkulatorische Zinsen = durchschnittlicher Wert ∗ kalkulatorischer Zinssatz
Beispiel
In einem Unternehmen soll eine neue Maschine mit Anschaffungskosten von 100.000 € und einer Nutzungsdauer von 5 Jahren gekauft werden. Statt diese Maschine mit Fremdkapital zu finanzieren, für das das Unternehmen Zinsen zahlen müsste, tätigt der Gesellschafter eine entsprechende Einlage aus seinem Privatvermögen, für das er sonst 10 % Zinsen erzielen könnte.
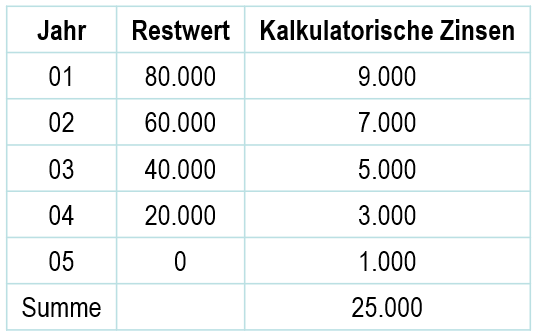
Die Maschine wird am 2. Januar 01 angeschafft und linear mit 20.000 € pro Jahr abgeschrieben. Zum Jahresanfang ist somit das gesamte Eigenkapital von 100.000 € in der Maschine gebunden.
Nun wird mit dieser Maschine die Herstellung und der Verkauf des Produktes P aufgenommen. Die kalkulatorischen Abschreibungen sind korrekterweise bei der Kalkulation des Produktpreises von P berücksichtigt, d. h. sie erhöhen den Produktpreis.
Wird P nun kontinuierlich im Lauf des Jahres verkauft, so sind am Ende des Wirtschaftsjahres dem Unternehmen liquide Mittel in Höhe der kalkulatorischen Abschreibungen von 20.000 € zugeflossen. Es hat also ein Mittelrückfluss von 20.000 € stattgefunden, die Kapitalbindung in der Maschine beträgt am Ende des Jahres nur noch 80.000 €.
Im Durchschnitt des ersten Nutzungsjahres beträgt die Kapitalbindung in der Maschine also (100.000 + 80.000) / 2 = 90.000 €.
Bei einem kalkulatorischen Zinssatz von 10 % beträgt die Höhe der kalkulatorischen Zinsen im ersten Jahr der Nutzung also 90.000 * 10% = 9.000 €.
Die gleiche Überlegung gilt nun auch für die folgenden Nutzungsjahre. Im zweiten Jahr der Nutzung beträgt die Kapitalbindung in der Maschine am Anfang des Jahres 80.000 €, am Ende des Jahres 60.000 €, im Durchschnitt des Jahres also 70.000 €. Bei einem kalkulatorischen Zinssatz von 10 % sind im zweiten Jahr der Nutzung also kalkulatorische Zinsen in Höhe von 7.000 € in Ansatz zu bringen usw.
Durchschnittswertmethode
Die Durchschnittswertmethode basiert auf der gleichen Überlegung, ihr Betrachtungszeitraum ist jedoch nicht jedes einzelne Jahr, sondern die gesamte Nutzungsdauer. Dabei ist ein evtl. verbleibender Schrottwert zu berücksichtigen.
Die Ermittlung der kalkulatorischen Zinsen mit Hilfe der Durchschnittswertmethode erfolgt also nach folgender Formel:
kalkulatorische Zinsen= (Anschaffungskosten + Schrottwert) / 2 ∗ kalkulatorischer Zinssatz
Beispiel (wie vor)
Am Anfang der Nutzungsdauer sind 100.000 €, am Ende der Nutzungsdauer 0 € in der Maschine gebunden, im Durchschnitt der gesamten Nutzungsdauer also (100.000 + 0) / 2 = 50.000 €.
Es kommen also jährlich 5.000 € kalkulatorische Zinsen zum Ansatz.
Die Summe der kalkulatorischen Zinsen über die Gesamtlebensdauer der abnutzbaren Anlagegüter ist bei beiden Verfahren gleich. Bei der Restwertmethode nehmen die kalkulatorischen Zinsen jedoch im Zeitablauf ab; die einzelnen Perioden werden also nicht gleichmäßig belastet, so dass unter der Annahme gleicher Produktionsbedingungen die Selbstkosten pro Stück von Jahr zu Jahr fallen. Bei der Anwendung der Durchschnittswertmethode sind dagegen die kalkulatorischen Zinsen im Zeitablauf konstant.
In der Praxis wird meistens die Durchschnittswertmethode bevorzugt, da
- sie einfacher als die Restwertmethode ist und
- sie Kontinuität in die Kalkulation bringt.
Ansatz des betriebsnotwendigen Kapitals
Da es nun in größeren Betrieben sehr aufwendig wäre, die kalkulatorischen Zinsen für jedes Wirtschaftsgut einzeln zu bestimmen, geht man in der Praxis zur Ermittlung der jährlich anzusetzenden kalkulatorischen Zinsen einen anderen Weg, indem man den kalkulatorischen Zinssatz auf das gesamte sog. „betriebsnotwendige Kapital“ des Unternehmens anwendet.
Dies erfolgt nach folgender Formel:
betriebsnotwendiges Vermögen
– Abzugskapital
____________________________
= betriebsnotwendiges Kapital
* kalkulatorischer Zinssatz
____________________________
= vorläufige kalkulatorische Zinsen
– effektiv geleistete Zinsen
= kalkulatorische Zinsen
Betriebsnotwendiges Vermögen
Zunächst wird aus der Finanzbuchhaltung das sog. „betriebsnotwendige Vermögen“ ermittelt. Ausgangspunkt bilden die Aktiva laut Bilanz des Unternehmens; dieses besteht aus dem Anlagevermögen und dem Umlaufvermögen.
Hiervon werden die nicht betriebsnotwendigen Teile abgezogen. Nicht betriebsnotwendig können z.B. sein
- Aktien, die der Anlage vorübergehend nicht benötigter liquider Mittel dienen
- Beteiligungen an anderen Firmen, die nichts mit dem eigentlichen Betriebszweck zu tun haben
- Grundstücke, die spekulativ gehalten werden (z.B. Bauerwartungsland)
Diesem Betrag sind die nicht in der Bilanz ausgewiesenen Vermögensbestandteile (sog. „stille Reserven“) hinzuzurechnen. Stille Reserven entstehen insbesondere dadurch, dass für Teile des Anlagevermögens
- höhere Abschreibungen angesetzt werden, als sie dem tatsächlichen Werteverzehr entsprechen,
- die Bewertung nach den historischen Anschaffungskosten erfolgt, der gegenwärtige Wert aber wesentlich höher ist.
Für die Ermittlung des betriebsnotwendigen Vermögens werden die durchschnittlichen Werte angesetzt, die sich aus der Eröffnungsbilanz zu Beginn des Wirtschaftsjahres (WJ) und am Ende des Wirtschaftsjahres ergeben:
Betriebsnotwendiges Vermögen = (Anfangsbestand + Schlussbestand) / 2
Abzugskapital
Von dem so ermittelten betriebsnotwendigen Vermögen wird nun das Abzugskapital abgezogen, Hierunter versteht man diejenigen Fremdkapitalteile, die dem Unternehmen tatsächlich zinslos zur Verfügung stehen. Dies sind z.B.
- zinslos erhaltene Lieferantenkredite,
- zinslose Gesellschafterdarlehen,
- Anzahlungen von Kunden,
- Rückstellungen und
- Rechnungsabgrenzungsposten.
Wichtig
Bei Lieferantenkrediten ist zu berücksichtigen, dass häufig Skonti gewährt werden, die eine Art versteckten Zins darstellen; daher zieht man den Skonto zumeist vom Bruttobetrag der Rechnungen ab.
Auch für das Abzugskapital werden grundsätzlich die durchschnittlichen Werte angesetzt:
Abzugskapital= (Anfangsbestand + Schlussbestand ) / 2
Betriebsnotwendiges Kapital
Durch die Subtraktion des Abzugskapitals vom betriebsnotwendigen Vermögen erhält man das betriebsnotwendige Kapital. Dies ist der Betrag, der insgesamt verzinslich aufgewendet werden muss, um das Unternehmen betreiben zu können.
Vorläufige kalkulatorische Zinsen
Durch Multiplikation des betriebsnotwendigen Kapitals mit dem kalkulatorischen Zinssatz ergeben sich die sog. „vorläufigen kalkulatorischen Zinsen“. Dies ist der Zinsbetrag, der insgesamt aufgewendet werden muss, um das Unternehmen betreiben zu können.
Vorläufige kalkulatorische Zinsen= betriebsnotwendiges Kapital ∗ kalkulatorischer Zinssatz
Kalkulatorische Zinsen
Schließlich sind von den vorläufigen kalkulatorischen Zinsen die Zinsen abzuziehen, die das Unternehmen effektiv für die Bereitstellung von Fremdkapital geleistet hat. Hierdurch soll vermieden werden, dass es zu einer doppelten Verrechnung dieser Zinsen kommt:
vorläufige kalkulatorische Zinsen
– effektiv geleistete Zinsen
= kalkulatorische Zinsen
Literaturhinweise
Ebooks
- Mumm, Mirja, Einführung in das betriebliche Rechnungswesen, online abrufbar mit Ihrem HFU-Account: http://dx.doi.org/10.1007/978-3-642-28273-7
- Plötner, Olaf; Sieben, Barbara; Kummer, Tyge-F.: Kosten- und Erlösrechnung, online abrufbar mit Ihrem HFU-Account: http://dx.doi.org/10.1007/978-3-642-11920-0
Printwerke
- Coenenberg, A.G.; Fischer, T.M., Günther, T.: Kostenrechnung und Kostenanalyse
- Freidank, C.-C., Fischbach, S.: Übungen zur Kostenrechnung
- Friedl, G.; Hofmann, C.; Pedell, B.: Kostenrechnung: Eine entscheidungsorientierte Einführung
- Kahlenberg, F.: Kostenrechnung: Grundlagen und Anwendungen
- Olfert, K.: Kostenrechnung